
 Flux RSS 
Nos partenaires 
|
Remontée de l’algorithme d’EuclideOn dispose de deux nombres entiers positifs premiers entre eux a > b, et on cherche un couple de nombres entiers (u,v) qui satisfasse l’équation : 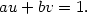
1 Petit rappel sur la division euclidiennePar division euclidienne, on désigne la division usuelle des entiers, telle qu’on l’apprend en primaire, non poussée. Par exemple, la division euclidienne de 255 par 7 donne : 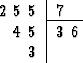
c’est à dire 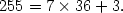
Le nombre 36 est le quotient de la division, et 3 en est le reste. 2 Remontée de l’algorithme d’EuclidePour deux entiers a > b premiers entre eux, on note a0 = a et a1 = b, et on commence par effectuer la division euclidienne de a0 par a1, 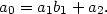 En effectuant les divisions euclidiennes successives de an par an+1, on construit ainsi deux suites (an)n et (bn)n d’entiers :
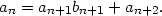 On peut montrer qu’en procédant ainsi, on arrive toujours à ak = 1 pour un certain indice k. A ce moment là, on arrête l’algorithme, et on va pouvoir le “remonter”. Pour remonter l’algorithme et trouver les coefficients de Bezout (u,v) dans 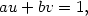 On y verra plus clair sur des exemples
3 Deux exemples
et on trouve finalement 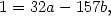 Version pdf de ce document : cliquez ici |
 Accueil
Accueil Droit
Droit Biologie
Biologie Chimie - Pharmacologie
Chimie - Pharmacologie Physique - Mécanique
Physique - Mécanique Ecologie - Géologie
Ecologie - Géologie  Informatique
Informatique  Linguistique/Histoire de l'Art médiévales
Linguistique/Histoire de l'Art médiévales  Sociologie
Sociologie  Mathématiques
Mathématiques  Progression de l'enquête
Progression de l'enquête
![1 = 3- 1× 2
1 = 3- 1× [53- 17 × 3]
1 = {a1 - 1× 53} - 1× [53 - 17× {a1 - 1× 53 }]
1 = {a1 - 1× (a0 - 2a1 )} - 1× [(a0 - 2a1 )- 17× {a1 - 1 × (a0 - 2a1)}]](Euclide27x.png)
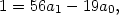

![1 = 97- 2 × 48
1 = 97- 2 × (145- 1× 97)
1 = [1402 - 9 × 145]- 2× (145 - 1 × [1402 - 9× 145])
1 = [1402 - 9 × {a1 - 1 × 1402}]- 2 × ({a1 - 1 × 1402} - 1× [1402- 9 × {a1 - 1× 1402}])
1 = [(a - 4a )- 9 × {a - 1 × (a - 4a )}]
0 1 1 0 1
- 2× ({a1 - 1× (a0 - 4a1)} - 1 × [(a0 - 4a1)- 9× {a1 - 1 × (a0 - 4a1)}]),](Euclide210x.png)