
 Flux RSS 
Nos partenaires 
|
Démonstration de la Proposition fondamentale du cryptage RSA.La compréhension de ce qui suit nécessite des connaissances en théorie des groupes. Commençons par un petit lemme qui se révélera très utile : Lemme 0.1. Soient G un groupe fini d’ordre n et d,e deux entiers tels que ed ≡ 1 mod (n). Alors les applications 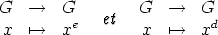 Démonstration : Il s’agit de vérifier que xed = x ∀x 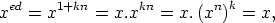 Notations : Nous disposons de deux nombres premiers p et p. On note 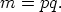  (ℤ∕mℤ) le groupe des inversibles de ℤ∕mℤ. On sait que le cardinal de
G est ♯G = φ(m) = (p - 1)(q - 1), où φ est l’indicateur d’Euler. On pose
donc (ℤ∕mℤ) le groupe des inversibles de ℤ∕mℤ. On sait que le cardinal de
G est ♯G = φ(m) = (p - 1)(q - 1), où φ est l’indicateur d’Euler. On pose
donc
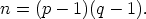 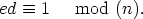 Démonstration : Nous devons vérifier que 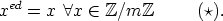  ℤ∕mℤ. Nous allons procéder par étapes : ℤ∕mℤ. Nous allons procéder par étapes :
Montrons maintenant que (⋆) est vérifiée pour tout x 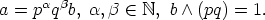 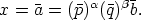
Conclusion : x s’écrit comme produit d’éléments vérifiant (⋆), ce qui prouve que x vérifie lui même cette relation, c’est à dire que xed = x dans ℤ∕mℤ. □ Version pdf de ce document : cliquez ici |
 Accueil
Accueil Droit
Droit Biologie
Biologie Chimie - Pharmacologie
Chimie - Pharmacologie Physique - Mécanique
Physique - Mécanique Ecologie - Géologie
Ecologie - Géologie  Informatique
Informatique  Linguistique/Histoire de l'Art médiévales
Linguistique/Histoire de l'Art médiévales  Sociologie
Sociologie  Mathématiques
Mathématiques  Progression de l'enquête
Progression de l'enquête
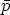 dans
dans 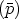
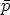 , c’est à dire que
, c’est à dire que 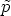 la classe de
la classe de 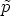
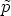
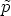 , c’est à dire que
, c’est à dire que 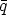 dans
dans 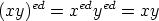
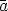 (dans
(dans 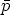 vérifie
vérifie 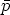
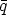
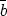
 vérifie
vérifie